Abstract
In this article we fit a time-dependent generalised extreme value (GEV) distribution to annual maximum flood heights at three sites: Chokwe, Sicacate and Combomune in the lower Limpopo River basin of Mozambique. A GEV distribution is fitted to six annual maximum time series models at each site, namely: annual daily maximum (AM1), annual 2-day maximum (AM2), annual 5-day maximum (AM5), annual 7-day maximum (AM7), annual 10-day maximum (AM10) and annual 30-day maximum (AM30). Non-stationary time-dependent GEV models with a linear trend in location and scale parameters are considered in this study. The results show lack of sufficient evidence to indicate a linear trend in the location parameter at all three sites. On the other hand, the findings in this study reveal strong evidence of the existence of a linear trend in the scale parameter at Combomune and Sicacate, whilst the scale parameter had no significant linear trend at Chokwe. Further investigation in this study also reveals that the location parameter at Sicacate can be modelled by a nonlinear quadratic trend; however, the complexity of the overall model is not worthwhile in fit over a time-homogeneous model. This study shows the importance of extending the time-homogeneous GEV model to incorporate climate change factors such as trend in the lower Limpopo River basin, particularly in this era of global warming and a changing climate.
Introduction
There is a general notion that the occurrence of extreme events has changed over these recent years and is anticipated to continue to change in terms of intensity, frequency and complexity of the risks. These recent changes are mainly attributed to global warming and natural modes of interannual and interdecadal variability, such as the El Niño phenomenon (Katz 2010; Katz, Parlange & Naveau 2002; Towler et al. 2010). The anticipated climate-induced changes are of major concern as they have the potential to render our estimates biased and/or useless, particularly those estimates based on traditional approaches that do not take climate changes into consideration. These probable climate changes can also cause negative societal impacts and disruptions, for instance, destruction of schools, children dropping out of schools leading to early marriages, particularly for girls, and thus creating a vicious poverty circle in the community (Katz 2010; Mudavanhu 2014). According to Katz (2010), previous studies in extreme value theory have shown that the frequency of all forms of extreme events, whether in the form of a single value or a sequence of annual maxima, is more sensitive to variations in the scale parameter (or, in particular, the standard deviation) than to the location parameter (or mean) of a distribution. Cooley (2009) wrote a commentary on the potential application of statistics of extremes to climate change based on the previous work of Wigley.
The annual maximum series (AMS), also known as block maxima, has long been employed to estimate the distribution of extreme events such as flood flows, precipitation and wind speeds. The time-homogeneous generalised extreme value (GEV) distribution, which uses standard properties of the likelihood function, has traditionally been used in designing flood estimation (Coles 2001; Maposa et al. 2014b; Towler et al. 2010). The use of a stationary GEV distribution assumes that climate changes and all other variables that may affect the validity of the estimation of design floods remain constant over time. In his wisdom, Gumbel (1941:187), the statistician and pioneer in the application of statistics of extremes to hydrology and other various fields, cautioned that:
In order to apply any theory we have to suppose that the data are homogeneous, i.e., no systematical change of climate and important change in the basin have occurred within the observation period and that no such change will take place in the period for which such extrapolations are made. (Katz 2010:71; Katz et al. 2002:188)
Without loss of generality, it is easy to understand that the assumption of homogeneity of climatic conditions and other important changes in the basin cannot hold forever. In other words, it is inevitable that climatic conditions change over time. The traditional fitting of the time-homogeneous GEV distribution also assumes that the observations are independent and identically distributed (i.i.d.). According to Katz et al. (2002), stationarity implies identicalness and not necessarily independence.
Dr Walter J. Ammann, chairman of the recent International Disaster and Risk Conference held in Davos, Switzerland, 24–28 August 2014, attested that the scope, intensity and complexity of risks as well as the frequency of natural hazards such as floods, earthquakes and forest fires are on the rise in these recent years (IDRC Davos 2014). The increase in the frequency of floods is also supported by a unique survey of 139 national meteorological and hydrological services carried out by the World Meteorological Organisation in 2013, which revealed that floods were the most frequently experienced extreme events worldwide over the course of the decade 2001–2010 (Mudavanhu 2014; WMO 2013). Floods and droughts account for 90% of all the people who are affected by natural disasters (Mudavanhu 2014; Smakhtin 2014). According to Munich Re (2013), the natural catastrophic statistics for the year 2013 was dominated by floods that caused billions of American dollars in losses. In Arya, Boen and Ishiyama (2014), the Director-General of UNESCO, Irina Bokova, stated that:
Every year, more than 200 million people are affected by natural hazards, and the risks are increasing – especially in developing countries, where a single major disaster can set back healthy economic growth for years. As a result, approximately one trillion dollars have been lost in the last decade alone. This is why disaster risk reduction is so essential. Mitigating disasters requires training, capacity building at all levels, and it calls for a change of thinking to shift from post-disaster reaction to pre-disaster action – this is UNESCO’s position. (p. 6)
Although it is clear from literature that the intensity and frequency of floods have increased over the recent years, it is not clear whether the magnitudes of floods, that is, flood heights, have also increased. If the magnitudes of flood heights have increased over the years, it is expected that the location parameter of the GEV, which is associated with the mean estimate of the distribution, should increase with increase in time. On the other hand, if there is no gradual increase in flood heights over the years and the sporadic extremely high floods are nearly or purely random, then we expect the scale parameter, which is associated with dispersion from the central location, to vary with time (Figure 1). Based on literature cited in the study, there is overwhelming evidence of covariates such as long-term trends or cycles in recent years attributed to man-made activities, which may lead to global warming and atmosphere–ocean circulation patterns such as the El Niño phenomenon, which undermine the long-held traditional assumption of stationarity (Towler et al. 2010; Vasiliades, Galiatsatou & Loukas 2015). Evidence of non-stationarity is exhibited in Figure 1 at all the three sites: Chokwe, Combomune and Sicacate of the lower Limpopo River of Mozambique. However, a visual inspection of Figure 1 shows no apparent trend. Figure 1 reveals that in the year 2000 flood height was a very rare extreme event at all the three sites.
 |
FIGURE 1: Time series plots of annual daily maximum (AM1) flood heights (in metres) at the three sites: (a) Chokwe (1951–2010), (b) Combomune (1966–2010) and (c) Sicacate (1952–2010) along lower Limpopo River of Mozambique. |
|
The present study considers a non-stationary time-dependent GEV distribution model whose location and scale parameters are expected to vary linearly or nonlinearly with time (Figure 1), whilst the shape parameter remains constant over time. This investigation is carried out for the lower Limpopo River basin (LLRB) of Mozambique. Detailed studies on the goodness of fit of the time-homogeneous GEV distribution in the basin are found in the studies by Maposa, Cochran and Lesaoana (2014a) and Maposa et al. (2014b). In the present study, we advocate for a statistical modelling approach based on maximum likelihood (ML) estimation in the possible presence of covariates. These covariates can be in the form of trends, cycles and physical variables such as El Niño (Katz et al. 2002). The covariate of particular interest in the present study is the trend. To the best of our knowledge, no similar work in the previous studies relating to statistics of extremes in a changing climate have been done for the LLRB of Mozambique.
According to Katz et al. (2002), although the probability weighted moments, also known as L-moments, are more popular in the application of hydrological extremes compared to ML estimation mainly because of their computational simplicity and better performance for small samples where ML is often inconsistent, the probability weighted moment technique has the demerit of being unable to readily incorporate covariates (see also Ferreira & De Haan 2015). On the other hand, the application of ML technique in the presence of covariates is straightforward in both block maxima and peaks-over-threshold (POT) approaches (Katz et al. 2002).
The outline of the rest of the article is such that Section 2 presents the research methodology, Section 3 presents the results and discussion of the findings, and finally Section 4 gives the concluding remarks.
Research methodology
The section presents the sequential steps taken to sort the data into the block maxima series (Ferreira & De Haan 2015), briefly discuss the probability framework of block maxima including the extension of time-homogeneous GEV model to linear and quadratic trend models.
Study sites and data
Mozambique National Directorate of Water, the authority responsible for water management in Mozambique in the Ministry of Public Works and Housing, provided the data used in the study. The data are hydrometric daily flood heights (in metres) recorded at the sites Chokwe (1951–2010), Combomune (1966–2010) and Sicacate (1952–2010), which are hydrometric stations for the lower Limpopo River of Mozambique (Maposa et al. 2014a, 2014b). The three sites are such that Combomune is located in the upper part of the basin about 162 km from the border with South Africa and Zimbabwe, Chokwe is located in the middle of the basin about 130 km downstream of Combomune and Sicacate is further downstream of Chokwe in the lower part of the basin on way to the sea.
Moving sums and block maxima
The raw data at the three sites were originally recorded as daily flood heights (or water levels). The data records at some sites stretch back to as far as 1930s. However, because of missing values, the records used in the study are for the period 1951–2010 for Chokwe, 1966–2010 for Combomune and 1952–2010 for Sicacate (Figure 1). In order to obtain AMS, sequential steps were taken to obtain the highest flood peak in each hydrological year (or block). Further steps were taken to obtain annual maximum (AM) flood heights of the moving sums of 2, 5, 7, 10 and 30 days. Finally, the following AM time series models were obtained: annual daily maximum (AM1), annual 2-day maximum (AM2), annual 5-day maximum (AM5), annual 7-day maximum (AM7), annual 10-day maximum (AM10) and annual 30-day maximum (AM30). The procedure to obtain these cumulative AM time series models was necessitated by the need to investigate whether the cumulative annual floods have any significant effect on the long-term linear or quadratic trend in location, scale or both.
In statistics of extremes, there are two fundamental approaches used in flood frequency analysis, namely, block maxima (or AMS) and POT (or partial duration series) (Ferreira & De Haan 2015). The approach used in the study is block maxima. In hydrological studies, when sample sizes are large, it is natural to block observations by years (Ferreira & De Haan 2015; Maposa et al., 2014b). The data used in this study have sufficiently large AM records extending over 40 years at each site. In flood frequency analysis, the block maxima approach is commonly used ahead of POT when data records have sufficiently large sample sizes and the data quality is adequate (Ferreira & De Haan 2015). The GEV distribution arises naturally when modelling block maxima, whereas for POT the generalised Pareto distribution is commonly used (Ferreira & De Haan 2015).
Extreme value models
Comprehensive details of probability framework of block maxima and the practical reasons for using block maxima over POT are given by Ferreira and De Haan (2015). Dombry (2013) proved the consistency of ML estimators when using block maxima approach.
We are already familiar with the background of extreme value theory, beginning with the limiting distributions of Fisher and Tippett (1928) and advanced theory and applications in Coles (2001). Let (Xi)i≥1 be i.i.d. random variables with common distribution function F ∈ D(Gξ) and corresponding normalisation sequences of constants am > 0 and bm such that:
where ξ is the extreme value index. Let Mk,m = max (X(k−1)m+1,…, Xkm), k ≥1, hence, n = m × k observations are divided into k blocks of size m, where n is the total number of observations (Ferreira & De Haan 2015). Then there exists a non-degenerate function G such that for a fixed block length m ≥ 1, the variables (Mk,m)k≥1 are i.i.d. with distribution function Fm such that:
As suggested by Eqn (2), an approximation of the distribution of Mk,m, or the distribution function Fm, is the GEV distribution with parameters am, bm and ξ estimated by the ML method in the study (Dombry 2013; Ferreira & De Haan 2015). The GEV cumulative distribution function, G, is given in Eqn (3) as:
where µ, σ and ξ are the location, scale and shape parameters, respectively. The model in Eqn (3) is the time-homogeneous GEV model. We shall call it model M0 and it shall be used as the reference model such that all other extended models are compared to it for their significance.
The log-likelihood function for the GEV in Eqn (3) for the case ξ ≠ 0 is given by Eqn (4):
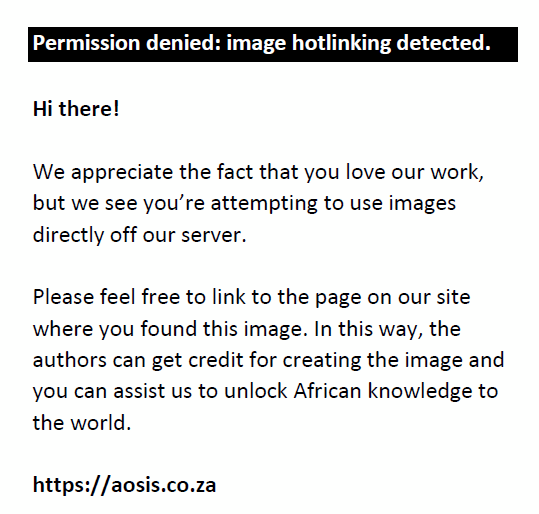
where k is the number of blocks (years) and x is AM.
Now consider the time-dependent GEV model, call it M1, with a linear trend in the location and the scale parameter such that µ(t) = µ0 + µ1 t, log σ(t) = σ0+σ1 t, and ξ(t) = ξ where t is time in years, then the general model is given in Eqn (5):
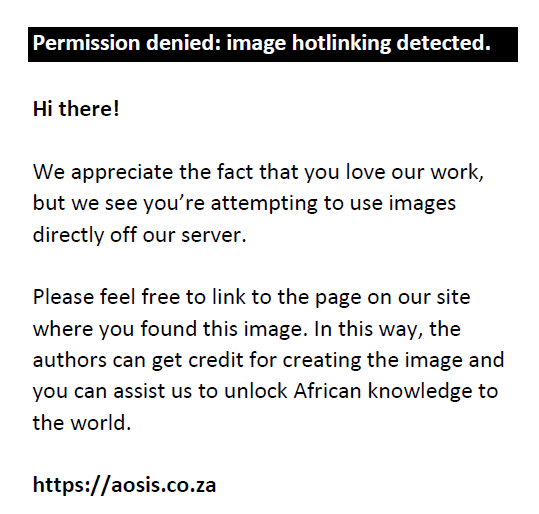
The log-likelihood function of model M1 for the case ξ ≠ 0 is given in Eqn (6) as:
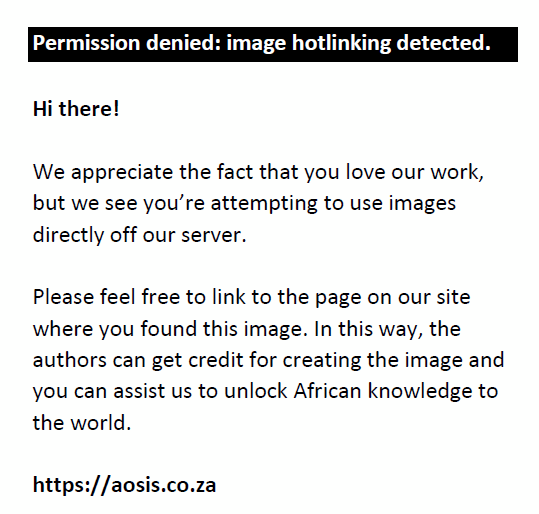
with the usual replacement when ξ = 0. The R package ismev is used to estimate the parameters of the GEV models (Heffernan & Stephenson 2015; R Core Team 2013).
In the present study, we also propose three more models, M2, M3, and M4. Model M2 has a linear trend in the location parameter such that µ(t) = µ0+ µ1(t), σ(t) = σ and ξ(t) = ξ, and hence model M2 and its log-likelihood are of the form G(µ(t), σ, ξ; x, t) and l(µ0, µ1, σ, ξ; x, t). As for the other two models, M3 has a linear trend in the scale parameter and M4 has a nonlinear quadratic trend in the location parameter such that µ(t) = µ, log σ(t) = σ0 + σ1t, ξ(t) = ξ and µ(t) = µ0 + µ1t + µ2t2, σ(t) = σ, ξ(t) = ξ for models M3 and M4, respectively. The model for M3 and its log-likelihood are of the form G(µ, σ(t), ξ; x, t and l(µ, σ0, σ1, ξ; x, t), respectively, whilst the model for M4 and its log-likelihood are of the form G(µ(t), σ, ξ; x, t) and l(µ0, µ1, µ2, σ, ξ; x, t), respectively.
Model choice
One important question to answer is whether the non-stationary model provides an improvement in fit over the time-homogeneous model M0; that is, is it worthwhile to have the non-stationary model? The ML estimation of nested models uses a simple procedure called the deviance (D) statistic to compare one model against the other. In the study, the time-homogeneous GEV model, M0, is a special case of the time-dependent models M1, M2, M3 and M4. In general, consider M0 ⊂ Mi,∀i=1,2,3,4, then we define deviance statistic, D, as in Eqn (7):
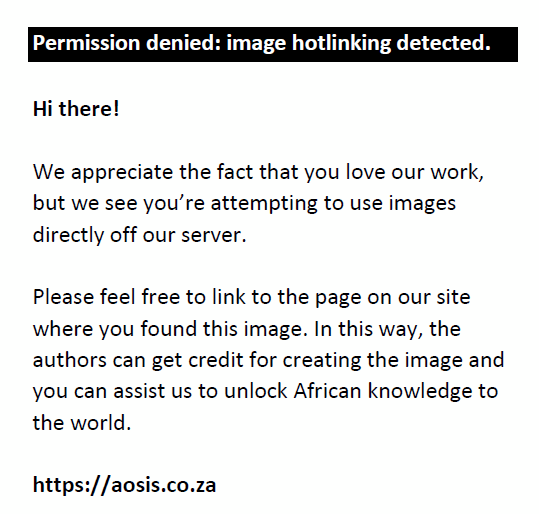
where li(Mi) and l0(M0) are the maximised negative log-likelihood for models Mi,∀i=1,2,3,4 and M0, respectively. D has a chi-square (χ2k,α) asymptotic distribution, with k degrees of freedom tested at α (=0.05 or 5%) level of significance, where k is the difference in dimensionality (or difference in number of parameters) of Mi and M0. Thus, D is compared to critical values of χ2k,α, where D > χ2k,α suggests that model Mi explains substantially more of the variability in the data than model M0.
Results and discussion
In order to avoid presenting too many tables in the article, only tables for the AM1 time series data are presented for each of the three sites Chokwe, Combomune and Sicacate in Tables 1, 2 and 3 respectively. The results for the AMS moving sums for each site are only discussed in detail if there is discrepancy with the AM1 results, else they are simply mentioned if there is consistency. The interested reader can obtain results for the AMS moving sums upon request from the corresponding author. The order of the models is maintained for the AMS moving sums, for example, for AM2 time series data model M1 still refers to a time-dependent GEV model with a linear trend in both the location and scale parameters as in AM1.
| TABLE 1: Annual daily maximum time-dependent generalised extreme value models for Chokwe for the period 1951–2010. |
| TABLE 2: Annual daily maximum time-dependent generalised extreme value models for Combomune for the period 1966–2010. |
| TABLE 3: Annual daily maximum time-dependent generalised extreme value models for Sicacate for the period 1952–2010. |
Chokwe models
Consider the pair of models (M0, M1) from Table 1, where M0 is taken as the reference model, χ22,0.05 = 5.991, D = 2(−125.802−(−126.313)) = 2(126.313−125.802) = 1.022 and the likelihood ratio test for m1= 0 has p-value = 0.4928 and for σ1= 0 has p-value = 0.1676 Because D is too small compared to the critical value (5.991) and the likelihood ratio test is not significant at the 5% level of significance (p-value > 0.05) for both the location and scale parameters, it clearly shows that the non-stationary model is not important and does not give any improvement in fit over the time-homogeneous GEV model. Similar insignificant results were obtained for the AMS moving sums AM2, AM5, AM7, AM10 and AM30 for model M1.
The other pairs from Table 1, (M0, M2) and (M0, M3), have D = 0.01 and 1.022, respectively, with a critical value of χ21,0.05 = 3.841 for both pairs. The likelihood ratio test for µ1 = 0 has p-value =0.4591 and σ1 = 0 has p-value = 0.1653 for M2 and M3, respectively, which is insignificant for both models at the 5% level of significance. The D statistic is again too small (< 3.841) for both models, implying that both models do not provide any improvement in fit over the time-homogeneous GEV model. Similar insignificant results were exhibited for the AMS moving sums AM2, AM5, AM7, AM10 and AM30 for models M2 and M3.
The quadratic model pair (M0, M4) in Table 1 has a D statistic value of 0.006 with a critical value of χ22,0.05 = 5.991, implying that model M4 does not provide any improvement in fit to justify its importance over the time-homogeneous model. The likelihood ratio tests for µ1 = 0 and µ2 = 0 are also not significant at the 5% significance level (p-value > 0.05). Again, similar results were obtained for AM2, AM5, AM7, AM10 and AM30.
In general, the results from Chokwe showed that the prevailing model for the site is the time-homogeneous GEV model given by Eqn (3). In other words, time is not an important factor for the AMS data at Chokwe. The general model estimate for Chokwe is given in Eqn (8):
where x = xi,∀i=1,2,…,k is the AM flood height. The diagnostic plots for the time-homogeneous model in Eqn (8) are presented in Figure 2. The diagnostic plots in Figure 2 show that the model is of good fit, with the exception of the year 2000 flood height which falls slightly outside the confidence limits.
 |
FIGURE 2: Diagnostic plots for the time-homogeneous generalised extreme value model at Chokwe hydrometric station: (a) Probability plot; (b) Quantile plot; (c) Return level plot; (d) Density plot. |
|
Combomune models
We start by considering the pair (M0, M1) from Table 2 with χ22,0.05 = 5.991, D = 5.36, and likelihood ratio test for µ1 = 0 has p-value = 0.2570. and for σ1= 0 has p-value = 0.0117. These results show that the linear trend in location parameter is not significant at the 5% significance level (p-value > 0.05), whilst the linear trend in scale parameter is significant (p-value < 0.05) in the model. In other words, the scale parameter is time dependent whilst the location parameter is time-homogeneous. However, the D statistic (5.36) is less than the critical value of 5.991 at 2 degrees of freedom, which implies that the non-stationary model M1 is not worthwhile compared to the time-homogeneous GEV model in Eqn (3). The same conclusions were reached for the moving sums of AM2, AM5, AM7, AM10 and AM30.
We now consider the pairs (M0, M2) and (M0, M2) from Table 2. The critical value for both pairs is χ21,0.05 = 3.841 with respective D statistic values of 0.252 and 4.928 for the two pairs. The likelihood ratio test for µ1 = 0 has p-value = 0.3092 and σ1 = 0 has p-value = 0.0141 for models M2 and M3, respectively. These results show that model M2 is not significant at the 5% significance level (p-value > 0.05) and is not worthwhile because D statistic value (0.252) is too small compared to the critical value (3.841). On the other hand, model M3 is significant at the 5% significance level (p-value < 0.05) and provides an improvement in fit over the time-homogeneous GEV model because the D statistic value of 4.928 (> 3.841) is significantly large. Similar findings were obtained for all the AMS moving sums.
The nonlinear quadratic model pair (M0, M4) has a D statistic of 0.226, which is too small compared to the critical value of 5.991 with two degrees of freedom. The likelihood ratio tests for µ1 = 0 and µ2= 0 are not significant at the 5% significance level (p-value > 0.05). Thus, the nonlinear quadratic model M4 is neither significant nor worthwhile over the time-homogeneous GEV model. Likewise, the same conclusions were reached for all the AMS moving sums.
Overall, the final model for Combomune is the non-stationary model, M3, with a linear trend in the scale parameter of the GEV. The general model for Combomune is given in Eqn (9):
where ti = τi−1965, τi = 1966, 1967, … and ti = 1, 2, 3, … is time in years and x = xi,∀i=1,2,…, is the AM flood height. The diagnostic plots for the time-heterogeneous model in Eqn (9) are presented in Figure 3. The residual probability plot suggests a good fit to the data.
 |
FIGURE 3: Diagnostic plots for the time-heterogeneous generalised extreme value model with a trend in the scale parameter at Combomune hydrometric station: (a) Residual probability plot; (b) Residual quantile plot. |
|
Sicacate models
The model pair (M0, M1) from Table 3 has χ22,0.05 = 5.991 and a D statistic value of 8.482. The likelihood ratio test for µ1 = 0 has p-value = 0.3217 and σ1 = 0 has p-value = 0.0045, which indicates that the linear trend in location parameter is not significant at the 5% significance level (p-value > 0.05), whereas the linear trend in scale parameter is highly significant (p-value < 0.05) in the model. Because the D statistic value (8.482) is greater than the critical value of 5.991, we conclude that model M1 provides an improvement in fit over the time-homogeneous GEV model; that is model M1 is worthwhile. These findings are consistent with findings from AMS moving sums AM2, AM5, AM7, AM10 and AM30.
The model pairs (M0, M2) and (M0, M3) in Table 3 share a critical value of χ21,0.05 = 3.841 with a D statistic value of 0.536 and 8.268 for M2 and M3 respectively. The likelihood ratio test for µ0 = 0 has p-value = 0.2638 and σ1= 0 has p-value = 0.0013 This indicates that model M2is insignificant at the 5% level of significance (p-value > 0.05) and not worthwhile (D < 3.841), whilst model M3 is highly significant at the 5% significance level (p-value < 0.05) and provides an improvement in fit over the time-homogeneous GEV model, with a large D statistic value of 8.268 (> 3.841). These findings are also consistent with findings from all the AMS moving sums.
The nonlinear quadratic model pair (M0, M4) in Table 3 has a D statistic value of 0.348 with a critical value of χ22,0.05 = 5.991 The likelihood ratio test for µ1 = 0 has p-value = 0.4991 and µ2 = 0 has p-value < 0.0001 This implies that the linear trend term in the location parameter is not significant at the 5% level of significance (p-value > 0.05) whilst the quadratic trend term in location parameter is highly significant (p-value < 0.0001). However, the overall nonlinear quadratic model is not worthwhile because the D statistic value of 0.348 is too small compared with the critical value of 5.991. Again, these findings are consistent with findings from all the AMS moving sums.
We now have two competing ‘good’, non-stationary, linear, time-dependent models for Sicacate. To identify the most appropriate of these models, we rate the one with the smaller standard errors and the smaller p-value as the most appropriate model. In this case, model M3 has a smaller p-value in the slope of the scale parameter 0.0013 compared to 0.0045 for M1, and the standard errors for M3 are much smaller than those of M1 for example 0.47428 compared to 0.64696 for µˆ0 and 0.01722 compared to 0.02249 for scale slope σˆ1 for m3 and M1, respectively. Therefore, the non-stationary linear trend in scale GEV model for Sicacate is given in Eqn (10) and the alternative model is given in Eqn (11) as follows:
where ti = τi –1951, τi = 1952, 1953,… and ti = 1, 2, 3,… is time in years and x = xi,∀i=1,2,…,k is the AM flood height. The alternative non-stationary linear trend in location and scale GEV model is given as follows:
where ti = τi – 1951, τi =1952,1953,… and ti = 1,2,3,… is time in years and x = xi,∀i=1,2,…,k is the AM flood height. The diagnostic plots for the time-heterogeneous models in Eqn (10) and Eqn (11) are presented in Figure 4 and Figure 5, respectively. The residual probability plots for both models suggest a good fit to the data.
 |
FIGURE 4: Diagnostic plots for the time-heterogeneous generalised extreme value model with a trend in the scale parameter at Sicacate hydrometric station: (a) Residual probability plot; (b) Residual quantile plot. |
|
 |
FIGURE 5: Diagnostic plots for the time-heterogeneous generalised extreme value model with a trend in both the location and scale parameters at Sicacate hydrometric station: (a) Residual probability plot; (b) Residual quantile plot. |
|
The interesting findings are that whilst most studies in other regions have found a dominant linear trend in the location parameter of the GEV distribution for some rivers (e.g. Katz et al. 2002), the study has found no evidence of a significant linear trend in the location parameter of the GEV distribution for the LLRB of Mozambique. On the other hand, the study has revealed a dominant time-dependent scale parameter for the river at Combomune upstream and Sicacate further downstream. The study also revealed evidence of a highly significant nonlinear trend, quadratic term, in the location parameter at Sicacate, although the complexity of the overall model was not worthwhile with reference to the time-homogeneous GEV model. The findings in the study are in full support of a previous study by Aich et al. (2014), who used a geoscientific model called eco-hydrological SWIM model to compare the climate change impacts on streamflow in four large African basins including the Niger, upper Blue Nile, Oubangui and Limpopo and found the Limpopo basin to be highly sensitive to climate change variability. The results obtained in the study complemented by those of Aich et al. (2014) explain the reason for the increased frequency of extreme floods in the LLRB of Mozambique, which can be attributed to the variability in climatic conditions. The time-dependent GEV models developed in the study are worth considering by the Mozambican government and its partners, as well as its neighbours, in their policies and decision making. Chokwe Irrigation Scheme, the largest irrigation scheme in Mozambique is situated in the LLRB, making the basin the backbone of the country’s economy, which is mainly characterised by agriculture and fishing.
Conclusion
The study considered the use of statistics of extremes in a changing climate for the LLRB of Mozambique. Three hydrometric stations representing three sites along the lower Limpopo River were considered for the study. The ML estimation method was used to estimate the parameters of the GEV distribution in the presence of a trend covariate. The study has revealed the importance of considering non-stationary linear and nonlinear trend models when using statistics of extremes in a changing climate as these models provide an improvement in fit over the time-homogeneous models. This improvement in fit is very important for the planning and policy-making of the government of Mozambique and its partners in the LLRB, where the largest irrigation scheme of the country is situated. The importance of the developed models is attributed to the fact that these non-stationary models take into account the reasons for increased frequency of floods in the basin. Once the government and its partners are fully aware of the reasons behind the increased frequency of floods in the basin, their planning can be much improved.
The study has successfully identified the prevailing models at the three sites such that Chokwe is the only site with a time-homogeneous GEV model. This can be attributed to the fact that some of the water at the site is diverted to the Chokwe Irrigation Scheme for irrigation purposes. The other two sites Combomune and Sicacate have a prevailing non-stationary GEV model with a dominant linear trend in the scale parameter. The site of Sicacate has an alternative non-stationary model with a linear trend in both the location and scale parameters of a GEV distribution. The prevailing models established in the study are consistent with cumulative (or moving sums) AMS flood flows and therefore appear reliable to use for flood frequency analysis in the basin. The use of the identified time-dependent GEV models with a trend in the scale parameter in the basin would also reduce the sensitivity of the frequency of floods, which is known to vary with changes in the scale parameter and therefore lead to more reliable estimates in the frequency of floods.
Future studies will attempt to advance the study to consider non-stationary generalised Pareto distributions, Bayesian inference and Markov chain Monte Carlo methods in a changing climate for the lower Limpopo River of Mozambique. Covariates in the form of cycles and/or a physical variable such as a dummy variable indicating the occurrence of cyclones in the region will also be considered in future studies involving statistics of extremes in a changing climate.
Acknowledgements
We thank the Mozambique National Directorate of Water and Mr. Isac Filimone of the Directorate, in particular, who provided us with all the necessary data used in the study. We are also indebted to United Nations Office for the Coordination of Humanitarian Affairs-southern Africa for providing us with weekly update reports of floods in southern Africa, particularly for the LLRB of Mozambique. We are also greatly indebted to the Department of Science and Technology – National Research Foundation Centre of Excellence in Mathematical and Statistical Sciences of South Africa who provided funds for the postgraduate studies. Lastly, we thank the University of Limpopo for their support in research.
Competing interests
The authors declare that they have no financial or personal relationships which may have inappropriately influenced them in writing this article.
Authors’ contributions
D.M. drafted the original manuscript, acquired and analysed the data and made interpretations. The work is part of the PhD thesis chapters for D.M. under the supervision of J.J.C. and M.L. J.J.C. critically revised the original manuscript and made final approval of the version to be published. M.L. also critically revised the original manuscript and made final approval of the manuscript to be published.
References
Aich, V., Liersch, S., Vetter, T., Huang, S., Tecklenburg, J., Hoffmann, P., Koch, H., Müller, N. & Hattermann, F.F., 2014, ‘Comparing impacts of climate change on streamflow in four large African river basins’, Hydrology and Earth System Sciences 18, 1305–1321. http://dx.doi.org/10.5194/hess-18-1305-2014
Arya, A.S., Boen, T. & Ishiyama, Y., 2014, Guidelines for earthquake resistant non-engineered construction, UNESCO, Paris.
Coles, S., 2001, An introduction to statistical modelling of extreme values, Springer-Verlag, London.
Cooley, D., 2009, ‘Extreme value analysis and the study of climate change: A commentary on Wigley 1988’, Climatic Change 97, 77–83.
Dombry, C., 2013, ‘Maximum likelihood estimators for the extreme value index based on the block maxima method’, ArXiv 1301.5611v1 [math.PR], viewed 14 March 2015, from http://arxiv.org/pdf/1301.5611.pdf
Ferreira, A. & De Haan, L., 2015, ‘On the block maxima method in extreme value theory: PWM estimators’, The Annals of Statistics 43(1), 276–298. http://dx.doi.org/10.1214/14-AOS1280
Fisher, R.A. & Tippett, L.H.C., 1928, ‘Limiting forms of frequency distribution of the largest or smallest member of a sample’, Cambridge Philosophical Society 24, 180–190.
Gumbel, E.J., 1941, ‘The return period of flood flows’, Annals of Mathematical Statistics 12, 163–190.
Heffernan, J.E. & Stephenson, A.G., 2015, ‘Ismev: R package version 1.40’, viewed 10 November 2015, from http://www.ral.ucar.edu/~ericg/softextreme.php
IDRC Davos, 2014, ‘Integrative risk management-the role of science, technology & practice’, 5th IDRC Davos 2014, Programme & Short Abstracts, Davos, Switzerland, August 2014, pp. 24–28. The IDRC Davos 2014 Conference Proceedings, viewed 14 March 2015, from http://idrc.info/outcomes/conference-proceedings/
Katz, R.W., 2010, ‘Statistics of extremes in climate change’, Climatic Change 100, 71–76. http://dx.doi.org/10.1007/s10584-010-9834-5
Katz, W.K., Parlange, M.B. & Naveau, P., 2002, ‘Statistics of extremes in hydrology’, Advances in Water Resources 25, 1287–1304.
Maposa, D., Cochran, J.J. & Lesaoana, M., 2014a, ‘Investigating the goodness-of-fit of ten candidate distributions and estimating high quantiles of extreme floods in the lower Limpopo River basin, Mozambique’, Journal of Statistics and Management Systems 17(3), 265–283. http://dx.doi.org/10.1080/09720510.2014.927602
Maposa, D., Cochran, J.J., Lesaoana, M. & Sigauke, C., 2014b, ‘Estimating high quantiles of extreme floods in the lower Limpopo River of Mozambique using model based Bayesian approach’, Natural Hazards and Earth System Sciences Discussions 2, 5401–5425. http://dx.doi.org/10.5194/nhessd-2-5401-2014
Mudavanhu, C., 2014, ‘The impact of flood disasters on children education in Muzarabani District, Zimbabwe’, Jàmbá: Journal of Disaster Risk Studies 6(1), Art. #138, 1–8. from http://dx.doi.org/10.4102/jamba.v6i1.138
Munich Re, 2013, Floods dominate natural catastrophe statistics in first half of 2013, Press Release, 9 July 2013. Munich Reinsurance, Munich.
R Core Team, 2013, R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, viewed 10 November 2015, from http://www.R-project.org/
Smakhtin, V., 2014, ‘Managing floods and droughts through innovative water storage solutions’, 5th IDRC Davos 2014, The IDRC Davos 2014 Conference Proceedings, viewed 14 March 2015, from http://idrc.info/outcomes/conference-proceedings/
Towler, E., Rajagopalan, B., Gilleland, E., Summers, R.S., Yates, D. & Katz, R.W., 2010, ‘Modelling hydrologic and water quality extremes in a changing climate: A statistical approach based on extreme value theory’, Water Resources Research 46, W11504. http://dx.doi.org/10.1029/2009WR008876
Vasiliades, L., Galiatsatou, P. & Loukas, A., 2015, ‘Nonstationary frequency analysis of annual maximum rainfall using climate covariates’, Water Resources Management 29(2), 339–358. http://dx.doi.org/10.1007/s11269-014-0761-5
WMO. 2013, Global climate 2001–2010: A decade of climate extremes – Summary report, WMO no. 119, World Meteorological Organization, Geneva, Switzerland.
|


